Benjamin Adric Dunn, an information scientist on the Norwegian University of Science and Technology, reveals me an image of inconsistently spaced dots organized vaguely just like the rocks at Stonehenge. The total sample is evident—not less than, to a human. “When we look at this, it’s obviously a circle,” he says. But an algorithm would doubtless battle to acknowledge this straightforward form. “It very often misses the big picture.”
Many scientific processes contain loops, or repetitions. A pc’s lack of ability to see these relationships is an issue for scientists who wish to determine round patterns inside enormous plenty of information factors. Data are sometimes visualized as dots floating in area, like stars within the evening sky. A dot may symbolize a bodily location, like the 2 numbers for longitude and latitude marking the place a ship is on the excessive seas. Genes can likewise be plotted in a mathematical area of many dimensions—lots of typically—in order that two genes with comparable DNA sequences might be represented by close by factors. The significance of a round sample throughout the information is determined by context. Circles in a ship’s place may point out that it’s misplaced, whereas circles inside genetic information could show an evolutionary relationship.
Often these starry skies of information factors are too complicated and high-dimensional to check with the bare eye. To detect circles, researchers require a set of directions exact sufficient for a pc to grasp. But many customary methods for information evaluation are primarily based on a sort of arithmetic generally known as linear algebra, which research straight traces and flat planes. To hunt out loops, researchers are as an alternative turning to topological information evaluation (TDA), which presents a radically completely different perspective.
In distinction to the comparatively easy and inflexible constructions that characterize linear algebra, TDA is grounded in topology, a department of arithmetic that research pliable, stretchy shapes. Because its practitioners assume that every one shapes are arbitrarily versatile, topology is commonly known as rubber sheet geometry.
Like the formation of constellations from stars, topological information evaluation helps mathematicians construct revealing shapes from scattered dots. Researchers start by utilizing the info factors as nodes or joints in a digital scaffolding, constructing complicated constructions that will lengthen by lots of of dimensions. The ensuing image comprises a lot of the essence of the unique information however in a extra tangible type. They examine these constructions utilizing a topological perspective—searching for options which might be preserved even when the scaffolding is stretched or bent.
Topology’s usefulness in information evaluation lies in its skill to disclose qualitative, reasonably than quantitative, properties. It identifies the points of the construction that persist even when there are random errors, or noise, within the underlying measurements. Noise usually jiggles the underlying information, however the topology stays the identical—revealing sturdy options of the system. “There are lots of instances in the real world where the data given to you are squishy,” says Robert Ghrist, a mathematician on the University of Pennsylvania. “So you’ve got to use squishy math.”
Mathematicians and scientists are actually working collectively to seek out uncommon topological shapes in an unlimited vary of information, representing something from organic processes with each day rhythms to the construction of drug molecules. Perhaps essentially the most intriguing of those investigations pertain to mind construction. Mathematicians have used topology to discover how neurons work together throughout prolonged areas of the mind, reacting to completely different environment and stimuli. In collaboration with neuroscientists, Dunn lately discovered that sure mind cells use a torus, the mathematical title for the floor of a doughnut, to map their atmosphere.

Doughnuts and Coffee Cups
Even although topologists contort rubber sheets for a dwelling, they’re very cautious to protect the variety of holes in them. They by no means punch a brand new gap or press closed an present one. There’s a traditional math joke {that a} topologist cannot inform the distinction between a doughnut and a espresso cup: they each have one gap.
Topologists classify holes primarily based on their dimension. A closed loop, just like the numeral 0, has a one-dimensional gap as a result of it’s fashioned by gluing collectively the ends of a one-dimensional line. Starting with a two-dimensional aircraft, like a sheet of paper, and taping up the sides will yield one thing like a hole ball, which has a two-dimensional gap.
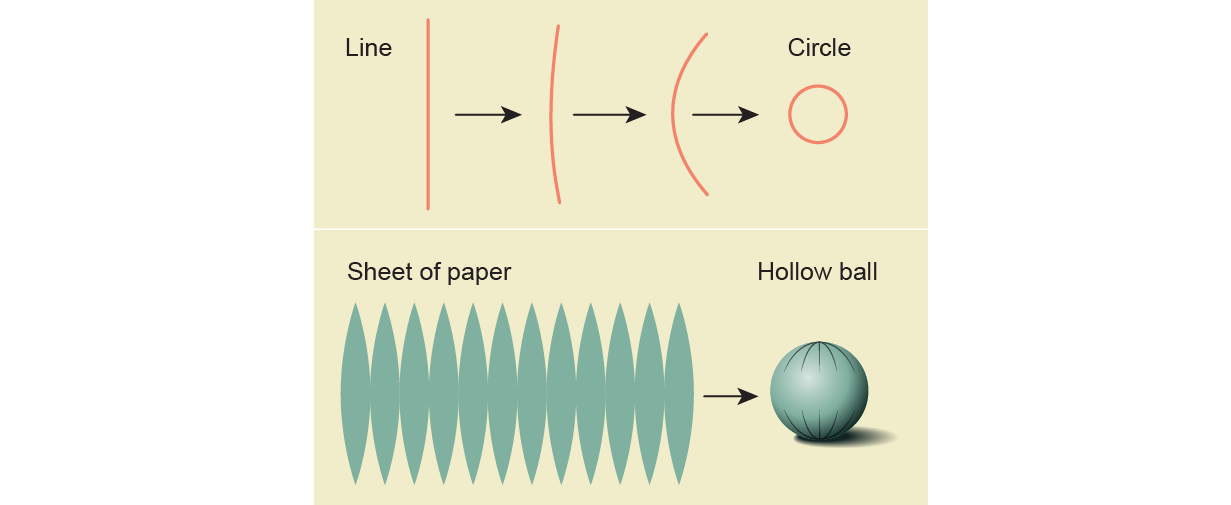
Higher-dimensional shapes can have higher-dimensional holes. By analogy with the one- and two-dimensional holes, for instance, a three-dimensional gap is fashioned by “closing up” a three-dimensional area, like a dice. But this course of could be seen solely from a four-dimensional perspective, exterior of most individuals’s—doubtless anybody’s—attain.
Some shapes have a number of holes of various dimensions, reminiscent of an inflatable ball with an hooked up deal with {that a} baby sits and bounces on. The hole middle of the ball is a two-dimensional gap, whereas the strong deal with varieties a one-dimensional gap. Topology has many exact strategies to rely holes in higher-dimensional shapes—a capability that seems to be useful in learning the mind’s neuronal exercise.
Neuroscientist Olaf Sporns of Indiana University thinks of the mind as a large transportation community. The roads and infrastructure are constructed from the neurons and their connecting synapses. The mind’s electrical and chemical indicators drive alongside these streets. “The physical roads constrain the traffic patterns that you can observe dynamically on top,” Sporns says. The visitors patterns change as we transfer and assume.
As we squint at a diagram of the mind, it’d seem like a group of factors, representing neurons. Some of them are related by traces, indicating a synapse between these specific neurons. Mathematicians discuss with this construction as a graph: a group of nodes related by edges. The graph flattens the organic complexity of the mind, however it retains the general form of the circuits. Such a trade-off is typical when making a mathematical mannequin, which weighs simplicity and analyzability in opposition to usefulness.
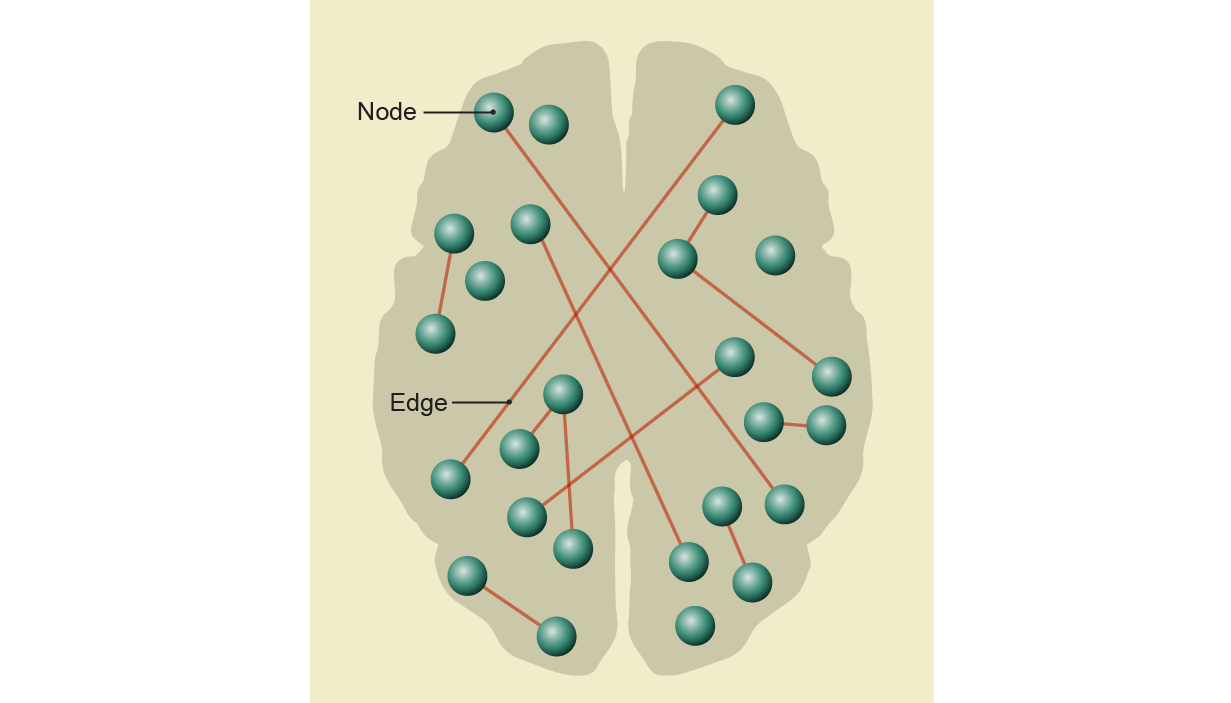
The graph of neuronal connections is a weblike mess: neurons are ample and richly interwoven. In 2017 Kathryn Hess, a mathematician on the Swiss Federal Institute of Technology in Lausanne, tackled this complication by doing one thing that’s initially shocking: she made the graph extra sophisticated. She analyzed information from the Blue Brain Project, a large pc simulation of the exercise of a rodent neocortex, part of the mind concerned in higher-order functioning. The pc mannequin comprises representations of the person neurons, that are related to different simulated neurons by way of synapses. These hyperlinks, in addition to when they’re more likely to fireplace, are decided by fundamental organic ideas and by experimental information from laboratory rodents.
The simulation can present the visitors patterns of the mind—the neurons firing in response to a stimulus. Unlike the aerial view of the true mind, nonetheless, the simulation could be paused, giving scientists a freeze body displaying which synapses are firing in response to a given stimulus. It is straightforward to transform this static picture right into a graph as a result of it signifies the info factors, in addition to the traces between them: two neurons are related if a synapse linking them is firing. From this image, Hess constructed one thing that mathematicians discuss with as a simplicial complicated, reworking the easy graph right into a voluminous form.
A simplicial complicated is constructed from triangles of various dimensions. In the Blue Brain graph, for instance, three neurons with all three synapses between them transmitting indicators fashioned the vertices of a hole triangle. To develop this construction right into a simplicial complicated, the mathematicians coloured on this hole triangle with a strong, two-dimensional triangle. Similarly, they stuffed in bigger clusters of related neurons with higher-dimensional analogs of triangles. For instance, a tetrahedron, a strong three-dimensional pyramid with 4 triangular faces, would fill in a bunch of 4 neurons firing collectively.
The most variety of neurons that Hess and others noticed firing as a bunch was eight, so the most important piece of this simplicial complicated was a seven-dimensional triangle. Many parts overlapped, forming a multidimensional sculpture: a triangle may jut out of a tetrahedron and meet one other triangle at a degree. Moreover, the mathematicians and scientists examined not only one however a collection of freeze frames, taken after simulating a mild stroke of the rodent’s whiskers. They transformed every of those maps right into a simplicial complicated and analyzed how its form modified in time utilizing the instruments of topology.
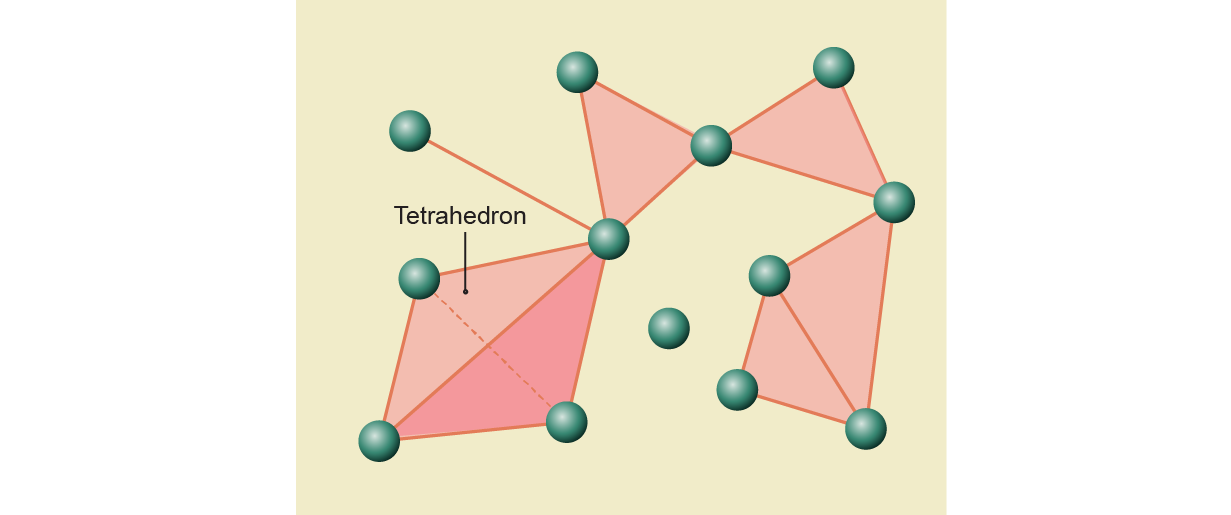
Immediately after receiving the stimulus, the simplicial complexes grew like a large Lego development, including in items of upper and better dimensions till the sculpture reached the utmost of three or 4 dimensions, relying on the stimulus. Then the entire thing quickly disappeared. “You have these increasingly complex structures that are being created by the stimulus until it just all collapses,” Hess says.
To a topologist, three traces related to make a triangle are the identical as a hole circle as a result of one form could be bent into the opposite. Because the simplicial complexes that Hess and her co-workers constructed from the simulated rodent brains are seven-dimensional, they’ll have holes in as much as seven dimensions. Their evaluation confirmed that as the form grew, the variety of holes elevated. At its peak, the construction contained a surprisingly giant variety of two- and three-dimensional holes—many greater than a random simplicial complicated or one constructed from a unique organic course of would yield. The particular sample of holes revealed a excessive degree of group within the neuronal response; this complexity could point out a elementary function of thought processes.
Stubborn Holes
More usually, nonetheless, information are represented by remoted factors floating in an summary mathematical area, with no apparent, preordained connections. To apply TDA, mathematicians want to determine the best way to join them. But there are various potential methods to hyperlink stars right into a constellation. To discover these implicit footage, mathematicians use a way generally known as persistent homology. Topologists analyze a succession of simplicial complexes constructed at numerous scales to seek out the important options of the info cloud.
To make the primary simplicial complicated, they solid the widest internet potential, connecting each level to each different level to type a dense mesh. Filling on this internet with strong varieties yields a high-dimensional simplicial complicated with few discernible options. But the mathematicians want to match this complicated with others fashioned by connecting the info at smaller scales. So, subsequent, they solid a narrower internet over the identical information, connecting solely close by factors. Now they’ve a sparser internet, which they use to assemble a second simplicial complicated. Because this mesh comprises fewer information factors, its simplicial complicated comprises shapes of decrease dimensions. The researchers repeat the method with a collection of smaller nets. “At every scale you’re going to have a different snapshot of what that complex looks like,” says Ranthony Edmonds, a mathematician on the Ohio State University.
Each simplicial complicated is a potential constellation fashioned with the identical scattered information dots. Topologists examine this spectrum of shapes—recording, particularly, the variety of holes in every dimension. They are particularly curious about holes that persist by many alternative scales. Some holes briefly seem after which disappear, however the cussed holes—those who survive by a variety of scales—level to essentially the most important options of the info. TDA can thus scale back a posh mess of information to a easy listing of cussed holes, in a lot the best way {that a} JPEG photograph file compresses a picture. “It’s a way of paring down the data to the stuff that really matters so that we have something much more workable,” Ghrist says.
Sometimes the holes recognized on this means have direct interpretations. Mathematician Jose Perea of Northeastern University and a staff of computational biologists used persistent homology to seek out periodic organic processes—those who repeat at common intervals. Examples embrace the metabolic cycle of yeast or a mouse’s circadian clock. “What is recurrence or repetition?” Perea asks. “Geometrically it should be like you’re traversing some sort of loop in the space of the thing that you’re looking at.”
TDA has additionally helped researchers design new medicine. These compounds are sometimes discovered by tweaking the molecular construction of present medicine. But the construction of molecules is extraordinarily complicated and troublesome to research, even for machine-learning algorithms. To design novel medicine, computer systems must work with simplified representations of the prevailing molecules. There are some ways to do that, however a staff led by Guowei Wei of Michigan State University selected to scale back molecules to their “topological signatures.” This is the outline of the chemical primarily based on its topological traits—basically the gathering of knowledge gained by persistent homology, such because the variety of cussed holes in every dimension.
Brain loops
The most intriguing utility of TDA could be on the most simple degree of mind group—a single sort of neuron. In 2014 John O’Keefe and analysis companions May-Britt Moser and Edvard Moser acquired the Nobel Prize in drugs for discovering, respectively, place cells and grid cells, kinds of neurons that activate when an animal is in particular areas. They act as sensors for place, says Carina Curto, a mathematician at Pennsylvania State University.
Each grid cell in a rat’s mind lights up when it’s in a number of locations inside its atmosphere. To determine the connection between the grid cells and the rat’s location, neuroscientists picked a single grid cell to check. They drew a dot on a pc mannequin of the ground, marking the place the rat was every time that cell activated. As the rat moved freely in regards to the sq. field, an everyday and repeating sample of dots emerged, of a sort that mathematicians describe as a hexagonal lattice. The dots on the lattice represented all of the areas the place that individual grid cell lit up. They repeated this course of with a number of grid cells, marking each in a unique colour. The dots corresponding to every grid cell had the identical total geometric sample however had been offset from each other, overlaying the field like busy tiling.
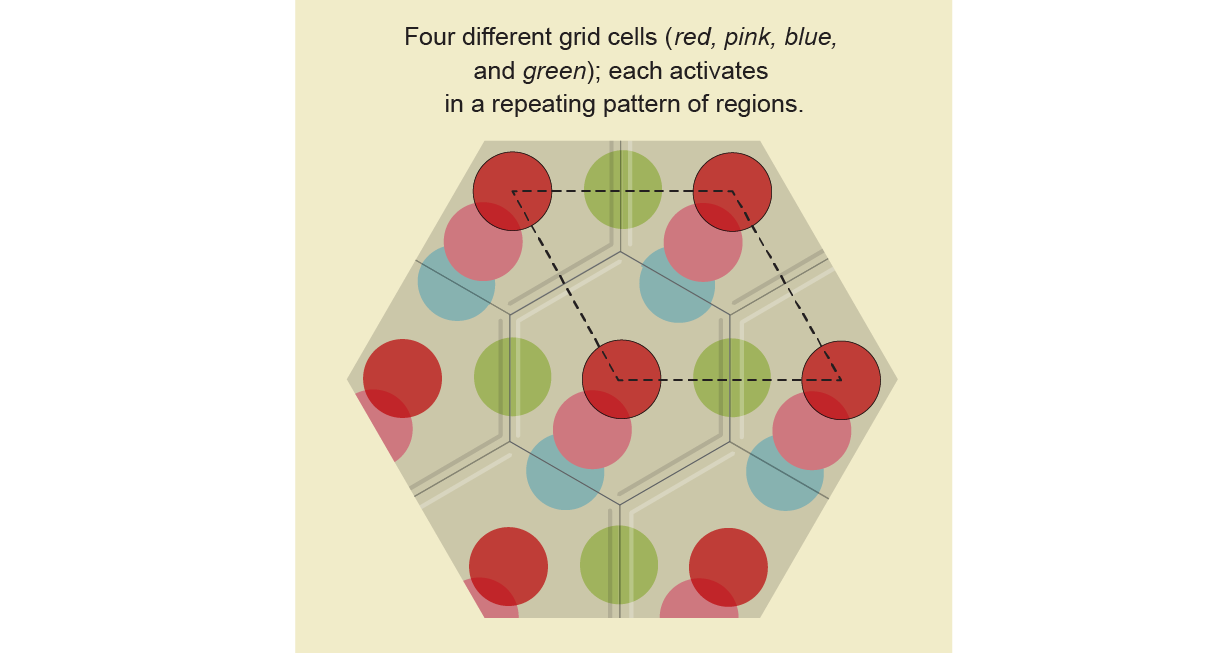
Neuroscientists wished to grasp precisely how the grid cells represented spatial areas—in essence, they had been searching for the template that produced the hexagonal sample. For instance, think about a round rubber stamp with numerous cartoon characters printed on it. As you roll out the stamp, it should create a line. The picture of Mickey Mouse will seem at common intervals alongside the road. But all these pictures got here from the identical location on the unique rubber stamp. It’s straightforward to think about rolling out a stamp, however the reverse query is tougher: How do you produce the template stamp from the sample that it created?
In the tiling of coloured dots representing the place the rat was when every grid cell fired, 4 neighboring crimson dots fashioned the corners of a slanted rectangle generally known as a parallelogram. Just just like the repeated pictures of Mickey Mouse, all of the crimson dots of the identical colour corresponded to a single grid cell. So topologists recognized all of the crimson dots, folding the parallelogram right into a doughnut form utilizing an operation they discuss with as “gluing.” First, they glued collectively two opposing sides of the parallelogram, forming a cylinder with two crimson dots: one on the highest and one on the underside. Next, they bent the cylinder, gluing collectively the 2 ends to type a torus. In this manner, the 4 crimson corners of the parallelogram develop into a single level on the doughnut. Exactly one dot of each different colour will present up on the torus. Thus, similar to the round stamp was the template for the road of cartoons, a torus is the right map for a way grid cells symbolize the ground of the field.
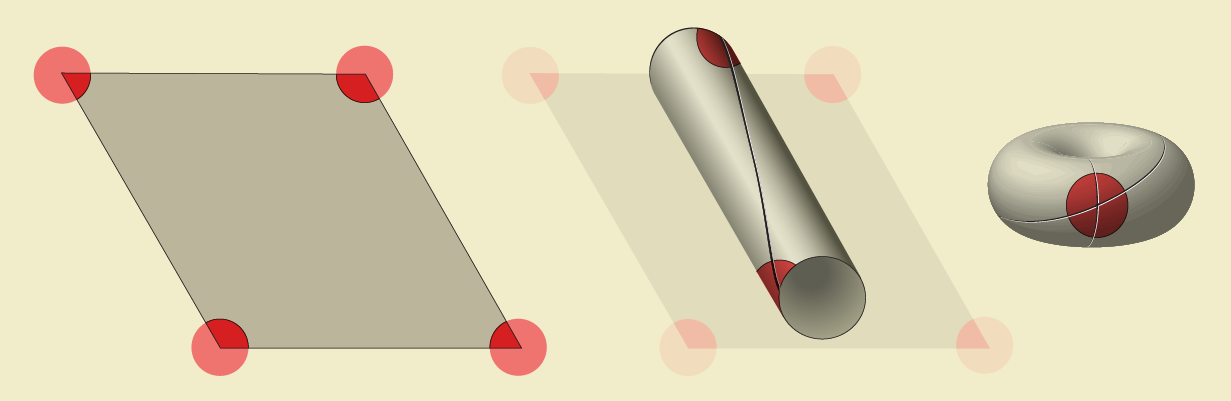
Neuroscientists may see this sample when the rat was operating round a field. But it was tougher to visualise the sample when the rat moved round different check fields, like a bicycle wheel with spokes and a central hub. Each grid cell was nonetheless firing in a number of positions, however scientists weren’t assured in regards to the underlying map. The association of dots was not clearly structured.
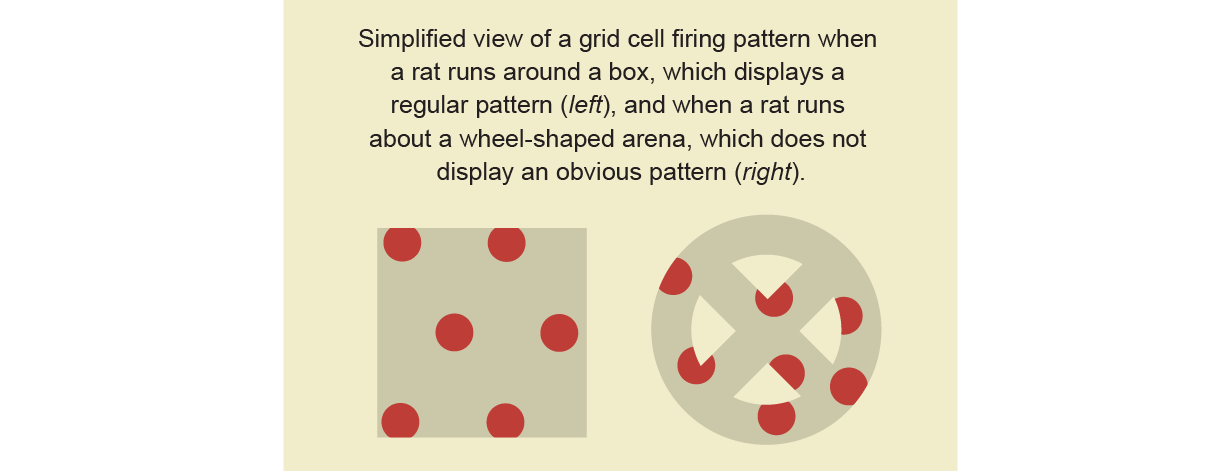
In a February 2022 Nature paper, a staff of mathematicians and neuroscientists, together with Dunn, used grid cells to check a idea known as steady attractor networks, which predicts that sure neurons are wired collectively in a selected sample—and the sample doesn’t change even when the animal is in a unique scenario. To check the speculation of steady attractor networks, researchers wanted to find out whether or not the grid cells all the time type a torus, it doesn’t matter what atmosphere the rat finds itself in. They had been trying to find tori in messy neurological information—the right job for TDA.
This time, as an alternative of marking the positions in a field the place a single grid cell fired, the researchers studied the collective exercise of a complete community of grid cells. At common intervals they recorded the state of the community utilizing a string of 0s and 1s, which indicated whether or not every grid cell was energetic or not. From a mathematician’s perspective, this lengthy string is a degree in a really high-dimensional area. In impact, because the researchers recorded the state of the system at completely different instants, they had been accumulating high-dimensional information factors. These factors describe the best way patterns of grid cell activation evolve in time, however the information are too sophisticated to check with the bare eye.
After utilizing some customary methods to simplify the info, the staff computed the persistent homology of the system by connecting the info factors at completely different scales and analyzing the ensuing simplicial complexes. As earlier than, the info fashioned a torus when the rat was operating a few field. But the true check was when the researchers derived information from a rat operating round a wheel-shaped area. To their delight, it once more fashioned a torus.
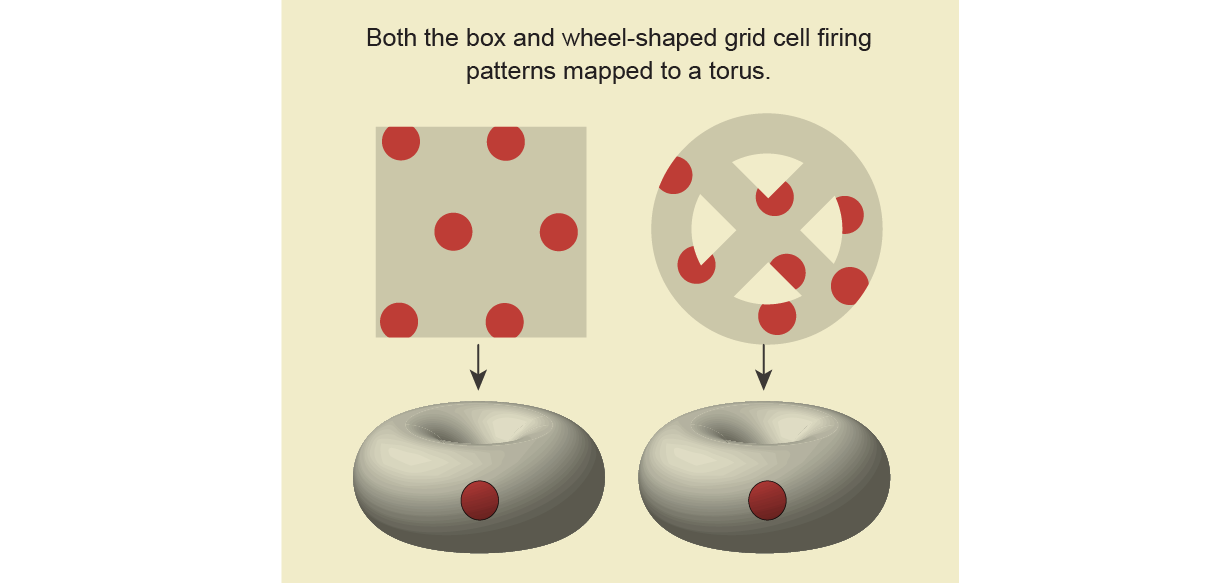
The researchers had been even capable of acquire information from a sleeping—probably dreaming—rat. Again, they discovered a torus, a form that persevered whatever the rat’s atmosphere or state of being, a discovering that helps the speculation of steady attractor networks. The doughnut form appears to be intrinsic to how grid cells symbolize area.
Many of those purposes of topological information evaluation are solely potential due to highly effective new computational instruments. “None of this would have happened if people hadn’t seriously started building algorithms,” says Vidit Nanda, a mathematician on the University of Oxford. “If it’s not effective, if it doesn’t scale well, then nobody wants to use it, no matter how beautiful the theory is.”
Thanks to those applied sciences, the makes use of of topology, which till lately gave the impression to be not more than an summary, if amusing, department of arithmetic, are burgeoning. “The applications are getting stronger and stronger,” says Gunnar Carlsson, a mathematician at Stanford University and one of many pioneers of TDA. “We’ve really crossed the chasm.”













Discussion about this post